More works from us

BC-MPPI: A Probabilistic Constraint Layer for Safe Model-Predictive Path-Integral Control
2025 Workshop on Agents and Robots for reliable Engineered Autonomy (AREA)
On the Benefits of GPU Sample-Based Stochastic Predictive Controllers for Legged Locomotion
2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)

Feedback-MPPI: Fast Sampling-Based MPC via Rollout Differentiation
Adios low-level controllers

Tommaso Belvedere1, Michael Ziegltrum2, Giulio Turrisi3, Valerio Modugno2
1CNRS, Université de Rennes, Inria, IRISA, Campus de Beaulieu, Rennes, France
2Department of Computer Science, University College London, London, UK
3Dynamic Legged Systems Laboratory, Istituto Italiano di Tecnologia (IIT), Genova, Italy
Paper Code arXiv
Feedback-MPPI teaser image

Abstract

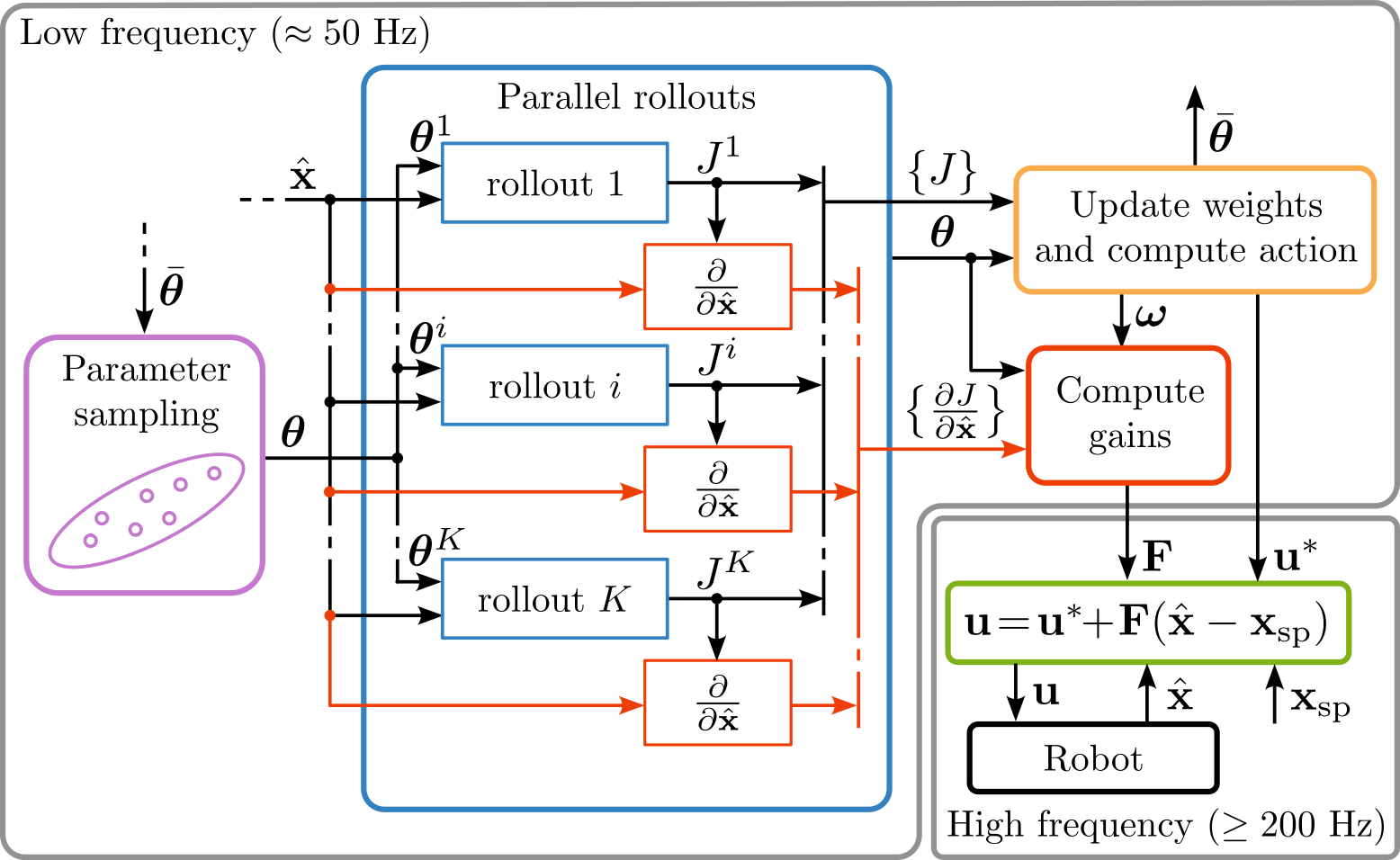
Model Predictive Path Integral control is a powerful sampling-based approach suitable for complex robotic tasks due to its flexibility in handling nonlinear dynamics and non-convex costs. However, its applicability in real-time, high-frequency robotic control scenarios is limited by computational demands. This paper introduces Feedback-MPPI (F-MPPI), a novel framework that augments standard MPPI by computing local linear feedback gains derived from sensitivity analysis inspired by Riccati-based feedback used in gradient-based MPC. These gains allow for rapid closed-loop corrections around the current state without requiring full re-optimization at each timestep. We demonstrate the effectiveness of F-MPPI through simulations and real-world experiments on two robotic platforms: a quadrupedal robot performing dynamic locomotion on uneven terrain and a quadrotor executing aggressive maneuvers with onboard computation. Results illustrate that incorporating local feedback significantly improves control performance and stability, enabling robust, high-frequency operation suitable for complex robotic systems.

BibTeX

@article{belvedere2026feedbackmppi,
      author={Belvedere, Tommaso and Ziegltrum, Michael and Turrisi, Giulio and Modugno, Valerio},
      title={Feedback-MPPI: Fast Sampling-Based MPC via Rollout Differentiation – Adios low-level controllers},
      journal={IEEE Robotics and Automation Letters},  
      year={2026},
      volume={11},
      number={1},
      pages={1-8},
      keywords={Robots;Trajectory;Costs;Real-time systems;Quadrupedal robots;Optimal control;Computational modeling;Standards;Legged locomotion;System dynamics;Optimization and Optimal Control;Motion Control;Legged Robots;Model Predictive Control},
      doi={10.1109/LRA.2025.3630871}
    }